Transcritical Bifurcations
In my last post, we discussed the simplest type of bifurcation, the saddle-node bifurcation. Next, we look at a different type of bifurcation. The transcritical bifurcation has the normal form
\[\begin{equation} \dot{x} = rx - x^2 \end{equation}\]In this type of bifurcation, instead of both fixed points annihilating each other, the fixed points “swap” stability. Let’s look at the normal form (1) to see what this means.

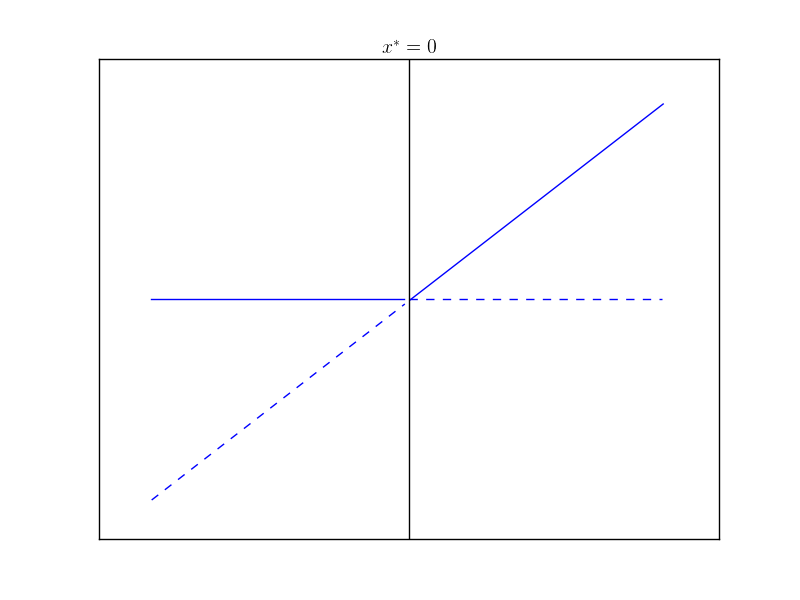
Notice that $x=0$ is a fixed point for a $r$. For $r<0$, $x = 0$ is stable and $x = r$ is unstable. For $r>0$ the fixed points “swap” stability and $x=0$ becomes unstable while $x=r$ is now stable. The bifurcation diagram is given next
Example
Next, we consider the example
\[\begin{equation} \dot{x} = rx - \log(1+x) \end{equation}\]We will handle this in two different ways. First, we look at the phase diagram of (2) for several values of $r$.
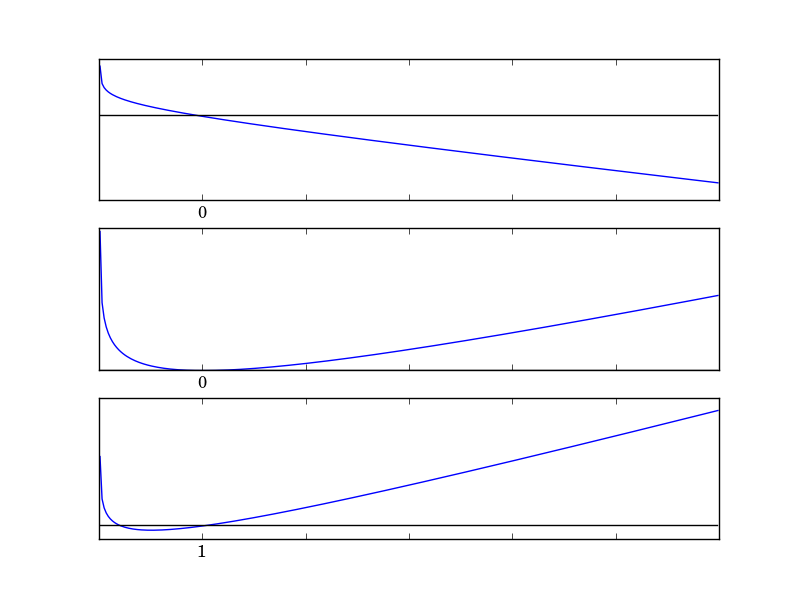
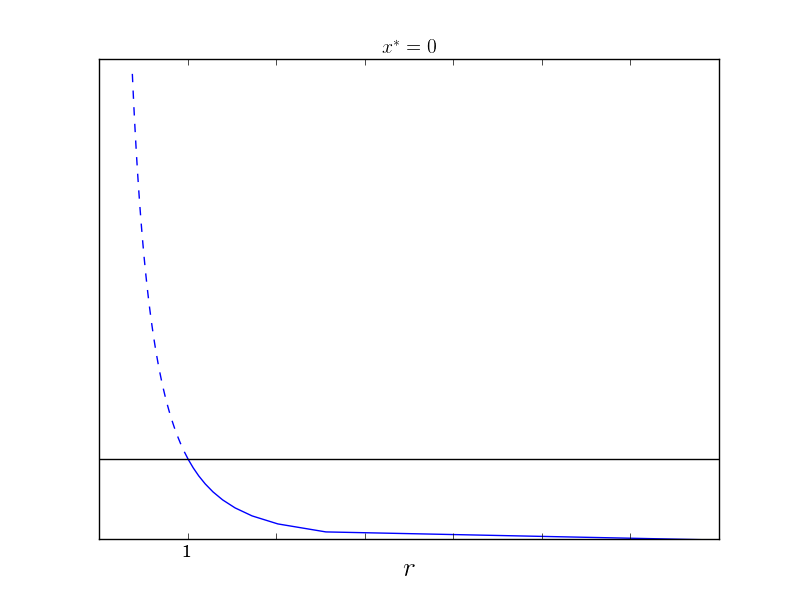
Notice that $x=1$ is a fixed point for all $r$. We can employ the same method as in the previous post and solve for $r$ in terms of $x$ and then just invert the axes. For a fixed point,
\[\begin{align*} 0 &= rx-\log(1+x)\\ r &= \frac{\log(1+x)}{x} \end{align*}\]When we invert the axes (making the plot of $x$ as a function of $r$) we get
Another strategy is to make use of the Taylor expansion of $\log(1+x)$ about the point $x=1$.
\[\log(1+x) = x - \frac{x^2}{2} + O(x^3)\]The the system (2) becomes
\[\begin{align*} \dot{x} &= rx - x + \frac{x^2}{2} + O(x^3)\\ &= (r-1)x + \frac{x^2}{2} + O(x^3) \end{align*}\]So
\[\begin{align} \dot{x} &\approx (r-1)x + \frac{x^2}{2}\\ \implies \dot{x} &\approx -2 (r-1)x - x^2 \end{align}\]Then again, the system has a trans-critical bifurcation at $r = 1$ and now a linear approximation of the bifurcation diagram (good for $x \approx 0$) is
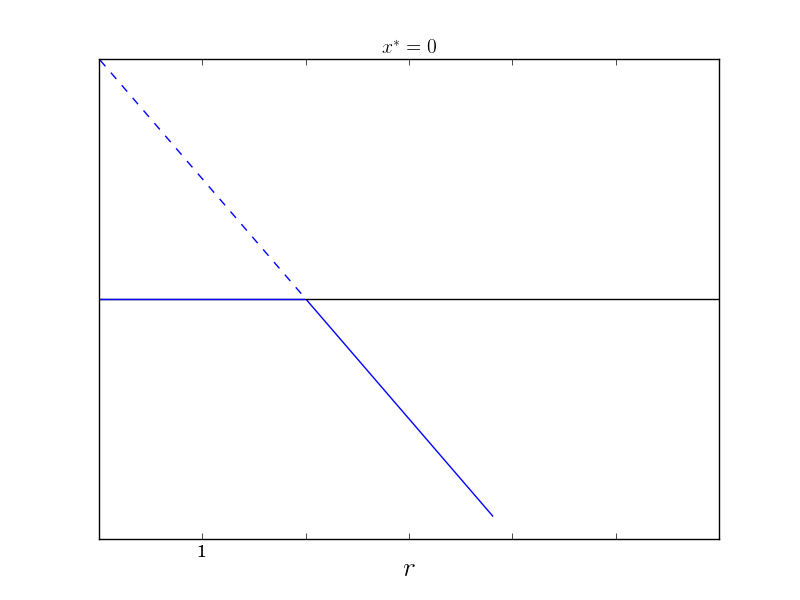
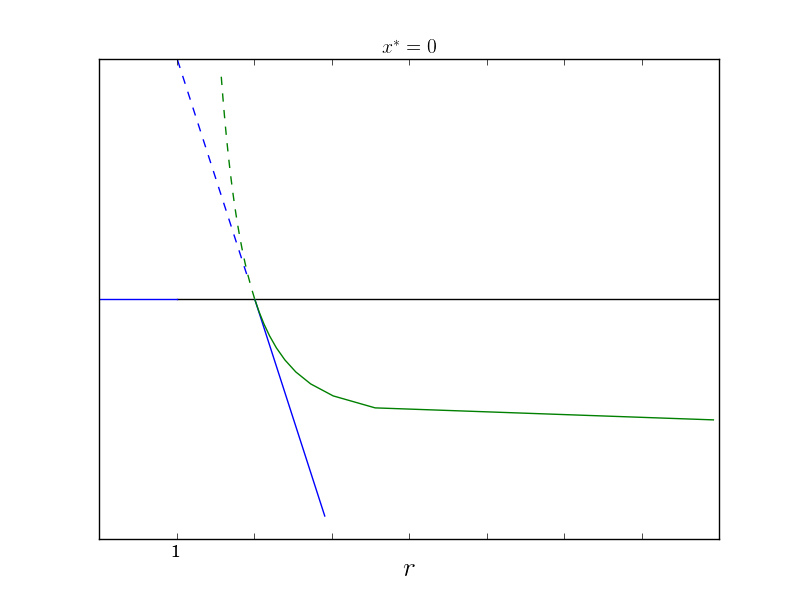
And here are the two plots together to get a better feel for how good the approximation is.
We have yet to discuss pitchfork bifurcations. It was my intention for that to be the topic of my next post. However, I recently started a new job working on the autonomous car at GM. Because of this, my area of focus will be shifting, so I don’t know if my current study of nonlinear dynamics will continue nor do I know what the topic of my next post will be. We shall see. I have written a post on pitchfork bifurcations linked above. This will likely be the end of the study of bifurcation theroy and non-linear dynamics for now.