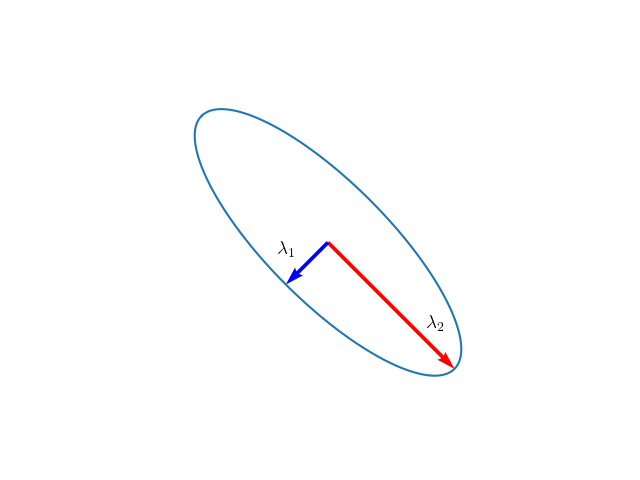
Quadratic Surfaces and the Eigen-Decomposition
An ellipsoid in $n$-dimensional space has the form
\[\begin{equation} \lambda_1x_1^2 + \lambda_2x_2^2 + \cdots + \lambda_nx_n^2 = 1 \end{equation}\]For example,
\[\frac{x_1^2}{a} + \frac{x_2^2}{b} = 1\]is the familiar equation of an ellipse in $\mathbb{R}^2$. Here $a = \frac{1}{\lambda_1}$ and $b = \frac{1}{\lambda_2}$ are the semi-major and semi-minor axes (taken together, these are called the principal axes).
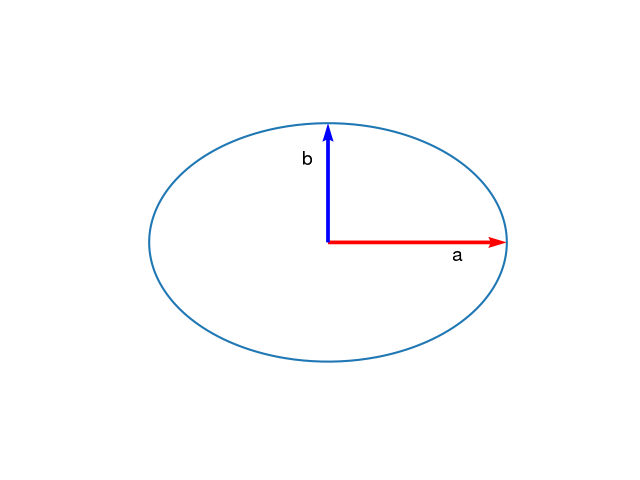
In the form above, the coordinates of the ellipsoid are aligned along the principal axes. However in a different frame of reference, the equation for the ellipse will contain cross terms. In $\mathbb{R}^2$, we will have an $x_1x_2$ term. In $\mathbb{R}^3$, we get three additional terms: $x_1x_2$, $x_1x_3$ and $x_2x_3$. In general, we will have $\frac{1}{2}n(n+1)$ terms instead of the $n$ we had in the first equation.
We need a systematic way to write the equation for a general $n$-dimensional ellipsoid. For this purpose, we will actually complicate matters a little bit by expanding to $n^2$ terms instead of the $\frac{1}{2}n(n+1)$ terms mentioned above by keeping distinct the products $xy$ and $yx$ (although they are obviously equal). The advantage of adding these terms are that we will be able to more clearly see the structure of the problem and it will help us analyze the situation more easily.
Let’s first look at the situation in $n=2$ dimensions.
\[\begin{aligned} a_{11}x_1^2 + a_{12}x_2x_1 + a_{21}x_1x_2 + a_{22}x_2^2 &= 1 \\ (a_{11}x_1 + a_{12}x_2x_1)x_1 + (a_{21}x_1 + a_{22}x_2)x_2 &= 1 \end{aligned}\]Now it becomes a little more clear why we were willing to pay the price of the extra terms (not combining $a_{12}x_2x_1 + a_{21}x_1x_2$ for instance in the 2-D case). This labeling convention for the coefficients elucidates the structure of the problem. In the general $n-$dimensional problem we get
\[\begin{aligned} &(a_{11}x_1 + a_{12}x_2+ \cdots + a_{1n}x_n)x_1 \\ +&(a_{21}x_1 + a_{22}x_2+ \cdots + a_{2n}x_n)x_2 \\ +&\cdots \\ &(a_{n1}x_1 + a_{n2}x_2+ \cdots + a_{nn}x_n)x_n \end{aligned}\]Then in matrix notation, the general quadratic surface in $n$-dimensional space has the form
\[\begin{equation} xAx = 1 \end{equation}\]The problem of aligning the principal axes of the ellipsoid (2) with the coordinate axes of the problem is thus a matrix diagonalization problem, i.e. an eigenvalue problem! In the coordinate system where the principal axes (eigenvectors of $A$) are the same as the coordinate axes, the equation (2) becomes (1) and the eigenvalues of $A$ become the entries along the diagonal.
For a point, $x$ lying on the ellipsoid (1) we have
\[xAx = 1\]If the point also lies on a principal axis, it satisfies
\[Ax = \lambda x\]Then, putting these two together
\[1 = xAx = x \lambda x\] \[\implies \lambda x^2 = 1\]so
\[\begin{equation} x^2 = \frac{1}{\lambda} \end{equation}\]The quantity
\[x^2 = x_1^2 + x_2^2 + \cdots + x_n^2\]is the distance from the center of the ellipsoid to the point $x$. The significance of the relation (3) is that it represents the distance from the center of the ellipsoid along the principal axis. Then, a large $\lambda_i$ means that in the direction $v_i$, the qudratic surface comes near to the center of the ellipsoid. A small $\lambda_i$ means that in the direction of $v_i$, the quadratic surface stays far from the center.