Why L1 Works, Simply
The problem of finding a sparse vector solution to an underdetermined system: \[\min ||x||_1 \text{ s.t. } Ax = f\] is known as the Basis Pursuit problem. This is also what is used in the extremely popular field of compressive sensing. Here \(A\) is an \(m \times n\) matrix with \(m \lt n\) (and usually \(m \ll n\)). When we say that the vector \(x\) is sparse, we mean it has few non-zero entries.
In this paper, Terrance Tao and Emmanuel Candes proved that it is possible to achieve near optimal recovery (accurate to within a given \( \epsilon \) ) using “very few” measurements (i.e. equations = rows in \(A\)).
I recently watched the plenary lecture Candes gave at The International Congress of Mathematicians. The talk was fascinating and I found it much simpler to understand than the first time I heard him speak when he came to town a few years ago; I recommend listening to it in its entirety. In his lecture, he provided the following simple explanation of why \(L^1\) optimization works.
We have a sparse vector, \(\vec x\) in \(L^2\):
 We also have a set of equations (just one equation since we are only working in two dimensions).
We also have a set of equations (just one equation since we are only working in two dimensions).
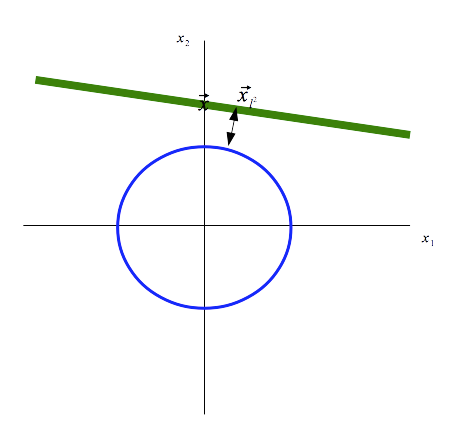
 If we look at the \(L^2\) ball we can more easily see the point on the line that has minimum
\(L^2\)-norm. This point is the one closest to the circle.
If we look at the \(L^2\) ball we can more easily see the point on the line that has minimum
\(L^2\)-norm. This point is the one closest to the circle.
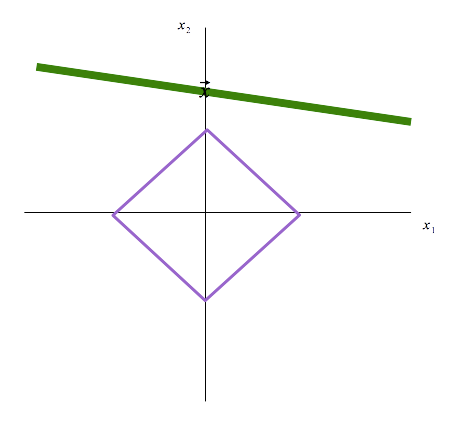
 You can see there is a bit of a discrepency between the goal vector \(\vec x\) and the vector with
minimum \(L^2\)-norm. Though the vectors look close, the difference is substantial when we start
working in higher dimensions. A good explanation
of the problem with distance functions in high dimensions is found near the beginning of this paper.
You can see there is a bit of a discrepency between the goal vector \(\vec x\) and the vector with
minimum \(L^2\)-norm. Though the vectors look close, the difference is substantial when we start
working in higher dimensions. A good explanation
of the problem with distance functions in high dimensions is found near the beginning of this paper.
Now, if we look at the \(L^1\) ball:
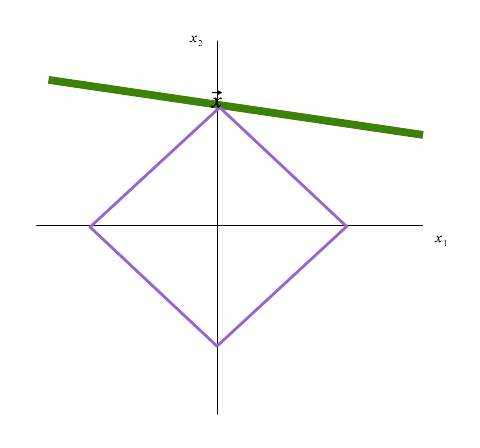
we notice that we get exact recovery (we get precisely the target vector \(\vec x\)) when we take the
vector on the line with minimum \(L^1\)-norm.
There is more to say about incoherence and taking a few extra samples to prevent trouble when we are in a less friendly situation, but I won’t include that here.
My work on this problem has revolved around Bregman Iteration and the faster Split Bregman Iteration developed by Yin et. al and Goldstein and Osher respectively. Specifically, I’ve looked at using their algorithm in the case when our vector \(x \in \mathbb C\).