Inverting a Constant Line in the Complex Plane
The day-to-day work of my new job does not afford me to study all the rigorous mathematics I may prefer. So, I have decided to keep my skills up by reading books on various topics of interest to me. Currently, I am studying Stephen Fisher’s Complex Variables as I heard good things about it a while ago.
During my reading, I came across this fascinating result
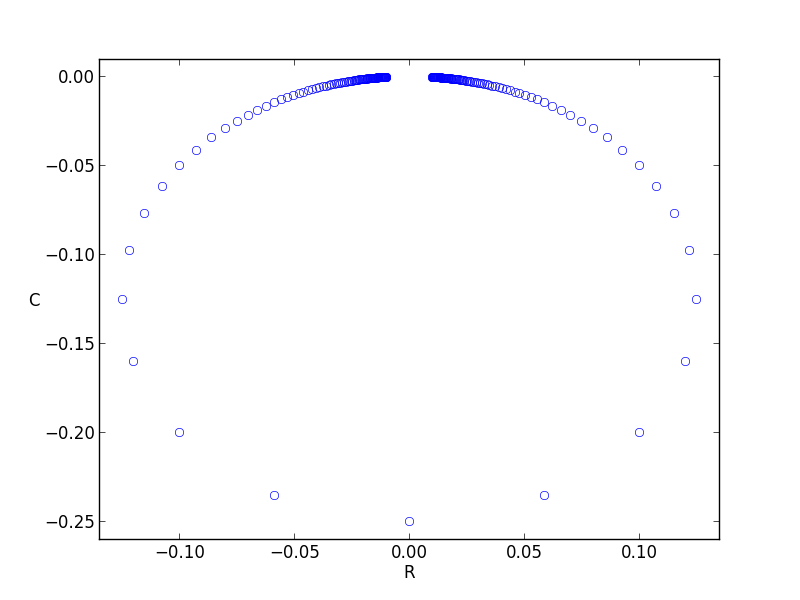
Proposition. Let \(L\) be the line \(y=a\), \(a>0\). Then the locus of points \(1/z\), \(z \in L\), is the circle of radius \(1/2a\) centered at \(-i/2a\).
Sure enough, if we write \(z= x + ia\) (since \(z \in L\)), then
\[\begin{align*} \left| \frac{1}{z} - \frac{-i}{2a} \right| &= \left| \frac{1}{x+ ia} + \frac{i}{2a} \right|\\ &= \left| \frac{2a + ix - a}{(x+ ia)2a} \right|\\ &= \left| \frac{a + ix}{(x + ia)2a} \right|\\ &= \frac{1}{2a} \left| \frac{a + ix}{x + ia} \right|\\ &= \frac{1}{2a} \end{align*}\]Since \(| z - z_0 | = \rho\) is an equation for a circle with radius \(\rho\), centered at \(z_0\) in the complex plane, the proposition is proven.
I also decided to plot this result because I found it so simple and yet surprising.
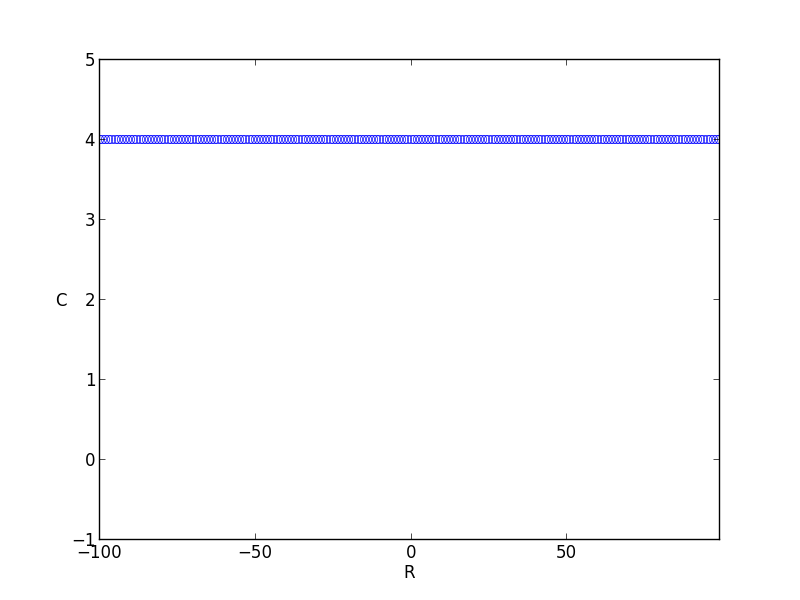
and then looking at \(1/z\) for \(z \in L\):