The Geometry of the SVD
The Singular Value Decomposition is one of the most prolific tools in applied mathematics. Many techniques for solving problems revolve around its computation. A lot of proofs can also be achieved by thinking “what happens if we take the SVD?” Yet, in spite of how important this tool is, I have just recently began to take a deeper look at the decomposition. Here we will look not at a formal proof of the existence and uniqueness of the SVD (though these are both true). Instead, we will just take an informal, geometric look at the decomposition.
The linear transformation, $A : \mathbb{R}^n \to \mathbb{R}^m$ represented by the $m \times n$ matrix $A$ maps the points lying on the unit sphere in $\mathbb{R}^n$ to a hyper-ellipse in $\mathbb{R}^m$. This statement is not obvious, but we will not prove it just now. Rather, we will see that the existence of the SVD proves this fact. At the beginning of this discussion, let’s assume that $A$ has full rank, $n$.
We make the following remarks on notation:
- let $S$ denote the unit sphere in $\mathbb{R}^n$
- $\sigma_1, \sigma_2, \ldots, \sigma_n$ will denote the singular values of $A$. That is, they are the lengths of the principle semiaxes of the hyperellipse $AS$. Note that it is customary to assume that the singular values are ordered such that $\sigma_1 \ge \sigma_2 \ge \ldots \ge \sigma_n$
- then, let ${u_1,u_2, \ldots, u_n } \in \mathbb{R}^m$ be unit vectors pointing in the direction of the principle semiaxes of $AS$. So $\sigma_1u_1$ is the largest semiaxis of the hyperellipse $AS$. These are the left singular vectors of $A$
- and finally, let ${v_1,v_2,\ldots, v_n} \in \mathbb{R}^n$ be unit vectors that are the preimages of the corresponding $u_i$. That is $Av_i = \sigma_iu_i$. These are the right singular vectors of $A$.
Here is a plot highlighting the above quantities for the matrix
\[A = \left[\begin{matrix}1 & 2 \\ 0&2\end{matrix}\right]\]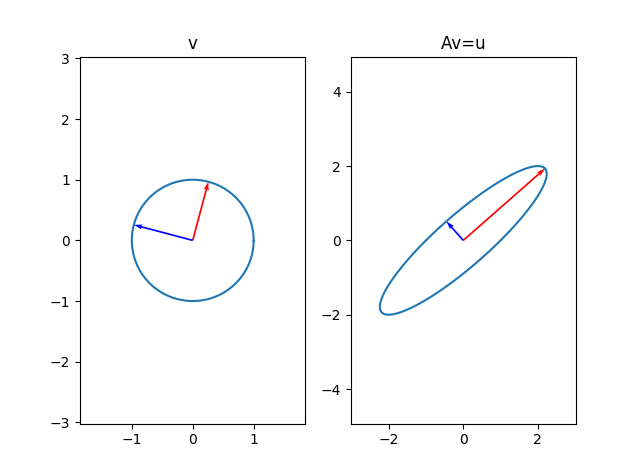
Reduced SVD
We can combine the vector equations
\[Av_i = \sigma_iu_i\]into the matrix equation
\[AV = \hat \Sigma \hat U\]where
\[\hat U = \left[\begin{matrix} \Bigg|&&\Bigg|\\ u_1&\cdots &u_n \\ \Bigg|&&\Bigg|\\ \end{matrix}\right]\]is an $m \times n$ matrix with orthonormal columns, $\hat \Sigma$ is a square diagonal matrix, and
\[V = \left[\begin{matrix} |&&|\\ v_1&\cdots &v_n \\ |&&| \end{matrix}\right]\]is an $n \times n$ matrix with orthonormal columns. Note that $V$ is unitary and thus invertible $\left(V^{-1} = V^*\right)$ so
\[\begin{equation} A = \hat U \hat \Sigma V^* \end{equation}\]This is the reduced singular value decomposition.
Full SVD
In the above formulation, $\hat U$ is not square unless $m=n$. So its columns do not form a basis of $\mathbb{C}^m$ and it is not unitary. However, if we adjoin $m-n$ orthogonormal columns to $\hat U$, it will become a square matrix $U$ with orthonormal columns, thus it is unitary. Then, to leave the factorization (1) unchanged, we just need to add $m-n$ rows of 0’s to the bottom of $\hat \Sigma$. Now we have an $m \times n$ matrix $\Sigma$ whose $n \times n$ upper block matrix is diagonal with entries $\sigma_1,\sigma_2,\ldots,\sigma_n.$
Then, the full SVD is the matrix decomposition
\[\begin{equation} A = U \Sigma V^* \end{equation}\]where
\[\begin{align*} U &\in \mathbb{C}^{m \times m} \text{ is unitary, }\\ V &\in \mathbb{C}^{n \times n} \text{ is unitary, }\\ \Sigma &\in \mathbb{R}^{m \times n} \text{ is diagonal }\\ \end{align*}\]Now it is clear that the image of the unit sphere in $\mathbb{R}^n$ is a hyperellipse in $\mathbb{R}^m$. The unitary matrix $V^*$ rotates and flips the vectors, $\Sigma$ stretches and shrinks the hyper-ellipse along its principle axes, and finally another unitary matrix, $U$ rotates and flips the hyperellipse. The proof that every matrix has an SVD proves that the image of the unit sphere under a linear map is a hyperellipse. We shall not prove this here.