Detecting a Phase Shift between Two Sine Waves
In applications, it can be useful to detect a phase shift in a signal relative to a certain reference. In this brief post, I will highlight one simple method of finding such a shift using a least squares approach.
Given a sine wave with a known phase, $\phi$ as a reference and a received sine wave, $\mathbf{f}$ with the same phase, but shifted by some $\delta$, we want to quickly find $\delta$.
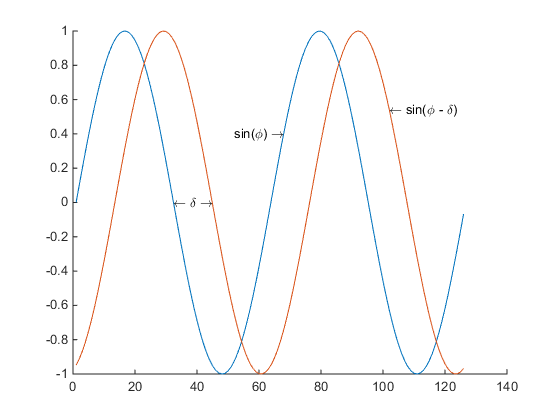
We permit the possibility of noise on our measurements.

Recall the difference of angles formula for sine
\[\begin{equation} \sin(\phi - \delta) = \sin\phi\cos\delta - \cos\phi\sin\delta \end{equation}\]Then, instead of a single measure of the phase, we can have a series of measurements for the phase of our reference, $\mathbf{\phi} = \left( \phi_1, \phi_2, \ldots, \phi_n\right)$. Then because of (1) we can form a basis from $\sin\mathbf{\phi}$, $\cos\mathbf{\phi}$, and $ \mathbf{1} = \left(1,1,\ldots,1\right)$ and write a system of equations,
\[\begin{equation} A\mathbf{x} = \mathbf{f} \end{equation}\]With the matrix
\[A = \left(\begin{matrix} \sin\phi_1 & \cos\phi_1 & 1\\ \sin\phi_2 & \cos\phi_2 & 1\\ \vdots & \vdots & \vdots\\ \sin\phi_n & \cos\phi_n & 1\\ \end{matrix} \right)\]and
\[\mathbf{x} = \left(\begin{matrix} \cos\delta\\ -\sin\delta\\ c \end{matrix}\right)\]The constant term allows for our signal to have some vertical shift.
The matrix equation (2) can be solved using least squares. Upon solving (2), notice that
\[\frac{-x_2}{x_1} = \frac{\sin\delta}{\cos\delta} = \tan\delta\]So our phase shift, $\delta$ is simply
\[\begin{equation} \delta = \arctan\left(\frac{-x_2}{x_1} \right) \end{equation}\]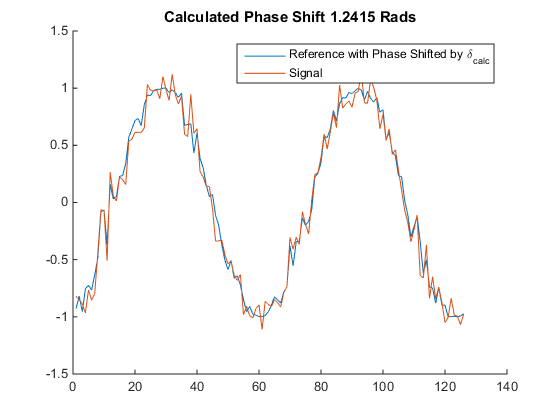
Note that while we do allow for a vertical shift in the sine wave, since our final answer only depends on the ratio of two entries in our vector, any amplitude scaling in our original model is unnecessary.