Fractal Dimension and its Application to Complex Networks
Much research has been done on the fractal properties of complex networks, most notably the seemingly contradicting ‘small-world’ phenomenon and ‘scale-free’ property. (You can find both articles as pdfs on the author’s website and the arxiv respectively.) In this post, we are going to look at where these ideas originated in Fractal Geometry and what we mean by self-similarity in a complex network. We will also define fractal dimension in the context of networks and finally look at how to compute the fractal dimension.
The emphasis of this post is not mathematical rigor. Rather, what is written here is an outgrowth of my understanding after spending about two weeks of study trying to solve a problem at work. With this being the case, the treatment is somewhat shallow (on the level of ‘what I need to know to solve a problem’) and geared more toward practical application. I have checked out a couple of books from the library on the subject of Fractal Geometry with a more mathematical bent. Perhaps there will be future posts on this topic that go more in depth.
Self Similarity
A defining characteristic of a fractal is self-similarity. By self-similarity, we mean that parts of the object are ‘the same’ as the object as a whole, just smaller. That is, we use the word ‘similarity’ in a way analogous to when we speak about similar triangles.
To illustrate the concept of self-similarity, consider the image below of the Sierpinski triangle.
(This image was taken from Wikipedia By Beojan Stanislaus, CC BY-SA 3.0.)
You can “zoom-in” on any one of the three smaller triangles by a factor of two and get the original image exactly. That is what we mean by ‘self-similarity’. The smaller triangles are an exact match (upon magnification) of the original triangle.
Fractal Dimension
The word ‘fractal’ was first introduced by Mandelbrot in his study of the length of the coast of Great Britain. In this paper, he defined what is meant by ‘self-similar’ as well as ‘fractal dimension’. The idea of fractal dimension (or fractional dimension) has to do with how much the measurement of the length of an object changes as the scale changes. It also captures the idea of how ‘space-filling’ a curve is.
The canonical example of a fractal observed in nature is measuring the coastline of a country. Take the images below for example. As the length of the ruler that we use shrinks, the total length of the coastline of Great Britain increases.
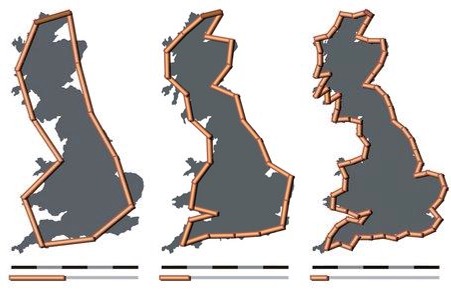
(This image also came from Wikipedia.) From left to right we have 11.5 rulers each 200 km long, then 28 rulers 100 km long each, and finally 70 rulers that are 50 km long each. The total length of the coastline of Great Britain increases in each case: 2300 km , 2800 km, and 3500 km respectively. The fractal dimension is a measure of how much the total length increases as the ruler shrinks.
While a country’s coastline is not a perfect fractal, we can use the Sierpinski triangle example from above as another example. Recall that we recover the original image if we zoom in on a third of the image by a factor of two. So we can define the fractal dimension of the Sierpinski triangle as
\[\begin{align*} FD &= \frac{\ln\left(\text{Number of self-similar pieces}\right)}{\ln \left(\text{Magnification factor}\right)}\\ &= \frac{\ln 3}{\ln 2}\\ &\approx 1.58 \end{align*}\]This is (nearly) precisely how Mandelbrot defined the fractal dimension. (Mandelbrot had the similarity ratio $r = \frac{1}{\sf Magnification\text{ } Factor}$ in the denominator which introduced a negative sign in his definition.) To further motivate the definition, he provided the following examples.
A line can be broken in half so that each part must be magnified by a factor of two to obtain the original. It can be broken into three equal parts which each need to be magnified by a factor of 3 to recover the whole, etc. In general, a line can be broken into $N$ equal pieces that can be magnified by a factor of $N$ to recover the original. So the dimension of a line in this sense is
\[\begin{align*} D &= \frac{\ln\left(\text{Number of self-similar pieces}\right)}{\ln \left(\text{Magnification factor}\right)}\\ &= \frac{\ln N}{\ln N}\\ &= 1 \end{align*}\]as we would expect. Similarly, a square may be broken into four self-similar pieces with magnification two, nine pieces with magnification factor 3, and $N^2$ pieces with magnification factor $N$. So that in general for the square
\[\begin{align*} D &= \frac{\ln\left(\text{Number of self-similar pieces}\right)}{\ln \left(\text{Magnification factor}\right)}\\ &= \frac{\ln N^2}{\ln N}\\ &= \frac{2\ln N}{\ln N}\\ &= 2 \end{align*}\]Again matching our intuition for what the dimension should be for a square. In general, whenever $ N^{\frac{1}{D}}$ is an integer, a $D-$dimensional parallelepiped can be broken into $N$ equal pieces with magnification factor $M=N^\frac{1}{D}$ so that
\[M=N^\frac{1}{D}\] \[\begin{equation} \implies D = \frac{\ln N}{\ln M} \end{equation}\]which is exactly how we defined fractal dimension above. Note that (1) can even be used for instances where $N^{\frac{1}{D}}$ is not an integer as is the case for the Sierpinski triangle.
Approximating Fractal Dimension
In applications, we want a way to approximate the fractal dimension of a body. The most common way to do this is by a so-called box-counting method. Several such methods exist and we will only describe the general idea.
Given a figure for which we want to approximate the fractal dimension, we begin by covering the area with boxes of side length $\epsilon$ and count the number of boxes, $N(\epsilon)$ needed to completely cover the area. We then cover the area in smaller boxes and count how many are necessary to cover the area with the new scale. We proceed in this way and define the box covering dimension ($BCD$) as
\[BCD = \lim_{\epsilon \to 0}\frac{\ln N(\epsilon)}{\ln \left(\frac{1}{\epsilon}\right)}\]mirroring the actual definition of fractal dimension given above.
Fractal Dimension in Complex Networks
Much like we can vary the length of our scale when measuring geometric objects, we can also change the ‘scale’ at which we look at complex networks. Song et.al proposed a box-covering method with which we can view a given complex network at different ‘scales’. From these different scales, we can then study the interconnectedness of clusters of nodes on different length scales. Thus giving a notion of how ‘self-similar’ the network is. We outline their idea next.
Given an undirected network, $G$, the algorithm selects a node at random and looks at all neighbors a distance $l_b$ away, $u_1, u_2, \ldots , u_{c_1}$ where the distance between nodes $u$ and $v$ is equal to the minimum number of edges required to get from $u$ to $v$. We then proceed to the next available node and repeat the process, giving us another list of nodes, $v_1, v_2, \ldots, v_{c_2}$. And so on. These groups of nodes are then grouped together to form a single node in the next graph. (The $c_1$ $u$’s become one node, the $c_2$ $v$’s form another, and so on.) The nodes in the resulting graph are then connected if a connection exists between any of the constituent nodes (the $u$’s and $v$’s) in the original network $G$. Thus, we have ‘renormalized’ the network and can look at it on a different ‘length’ scale. We can then repeat the process for the resulting network to view the network at varying scales.
We emphasize that by ‘self-similarity’, we do not mean that certain sub-graphs are isomorphic within $G$. Nor do we speak of the generalization of self similarity referred to as graph self-similarity. Rather, we mean that the graph formed by the renormalization procedure described above has the same degree distribution as $G$ (the original graph).
Through this post, I have tried to synthesize several topics that I have just been introduced to in the last couple of weeks. It would be remiss of me to not mention some of the sources that I have relied upon the most. Robert L. Devaney from Boston University has put together some nice introductory material on self-similarity and fractal dimension. These papers by Sarkar and Chaudhuri and Li et.al were two that helped clarify what we mean by fractal dimension and discussed two box-counting algorithms. I also relied heavily on the relevant pages from Wikipedia and the resources and papers that have been linked throughout this post.